লুকাস-কারমাইকেল সংখ্যা

আমরা জানি, ৩৯৯ = ৩ x ৭ x ১৯৷ এখানে ৩৯৯-এর তিনটি উত্পাদক হচ্ছে ৩, ৭ ও ১৯৷ এবং লক্ষণীয়, এ তিনটি উত্পাদকই মৌলিক সংখ্যা, কারণ ৩, ৭ ও ১৯ কে শুধু সংশ্লিষ্ট নিজ নিজ সংখ্যা ছাড়া আর কোনো সংখ্যা দিয়ে ভাগ করা যায় না৷ এগুলো হচ্ছে মৌলিক উত্পাদক৷ ইংরেজিতে এ ধরনের উত্পাদকের নাম Prime factor৷

এখন এই ৩৯৯ এবং ৩, ৭, ১৯ এই সংখ্যা চারটির প্রত্যেকটির সাথে ১ যোগ করলে আমরা পাবো ৩৯৯+১ = ৪০০, ৩+১ =৪, ৭+১ = ৮, ১৯+১ = ২০৷ এখন নতুন পাওয়া সংখ্যা ৪০০, ৪, ৮ ও ২০ -এর বেলায় লক্ষ করলে দেখা যাবে ৪, ৮ কিংবা ২০ হচ্ছে ৪০০-এর এক একটি উত্পাদক৷ অর্থাৎ ৪০০ সংখ্যাটি ৪, ৮ কিংবা ২০ দিয়ে বিভাজ্য৷

একইভাবে ৯৩৫ সংখ্যাটির বেলায় ৯৩৫ = ৫ x ১১ x ১৭, যেখানে ৫, ১১ ও ১৭ হচ্ছে ৯৩৫-এর একেকটি মৌলিক উত্পাদক৷ এখন ৯৩৫+১ = ৯৩৬, ৫+১ =৬, ১১+১ =১২ এবং ১৭ +১ = ১৮৷ লক্ষণীয়, প্রদত্ত মৌলিক উত্পাদক তিনটির সবগুলোর সাথে ১ যোগ করে পাওয়া তিনটি সংখ্যা ৬, ১২ এবং ১৮ মূল সংখ্যা ৯৩৫-এর সাথে ১ যোগ করে পাওয়া সংখ্যা ৯৩৬-এর একেকটি উত্পাদক৷ অর্থাৎ ৯৩৬ সংখ্যাটি ৬, ১২ এবং ১৮ দিয়ে আলাদা আলাদাভাবে নিঃশেষে বিভাজ্য৷ এ ধরনের গুণাবলীসম্পন্ন সংখ্যার নামই হচ্ছে লুকাস-কারমাইকেল সংখ্যা৷ উপরে দেয়া উদাহরণ দুটিতে ৩৯৯ ও ৯৩৫ হচ্ছে দুটি Lucas-Carmichael নাম্বার৷

লুকাস-কারমাইকেল সংখ্যার একটি সংজ্ঞা আমরা এভাবে দিতে পারি৷ যদি n একটি ধনাত্মক পূর্ণসংখ্যা হয়, এবং p যদি এ সংখ্যাটির একটি মৌলিক উত্পাদক বা প্রাইম ফ্যাক্টর হয়, তবে n+১ সংখ্যাটি অবশ্যই P+১ সংখ্যা দিয়ে নিঃশেষে বিভাজ্য হবে৷ অর্থাৎ P+১ হবে n+১-এর একটি উত্পাদক৷ প্রথা অনুসারে, একটি সংখ্যাকে শুধু তখনই লুকাস-কারমাইকেল নাম্বার হিসেবে ধরা হবে যদি সংখ্যাটি হয় বেজোড় এবং বর্গমুক্ত বা স্কয়ার ফ্রি৷ অর্থাৎ সংখ্যাটি কখনো কোনো মৌলিক উত্পাদক বা প্রাইম ফ্যাক্টরের বর্গসংখ্যা দিয়ে নিঃশেষে বিভাজ্য হবে না৷

গণিতবিদরা দেখছেন ৩৯৯-ই হচ্ছে সবচেয়ে ছোট লুকাস-কারমাইকেল সংখ্যা৷ প্রথমদিকের কতগুলো লুকাস-কারমাইকেল সংখ্যা ও এগুলোর উত্পাদক অর্থাৎ মৌলিক উত্পাদক নিচে উল্লেখ করছি৷

৩৯৯ = ৩ X ৭ X ৯
৯৩৫ = ৫ X ১১ X ১৭
২০১৫ = ৫ X ১৩ X ৩১
২৯১৫ = ৫ X ১১ X ৫৩
৪৯৯১ = ৭ X ২৩ X ৩১
৫৭১৯ = ৭ X ১৯ X ৪৩
৭০৫৫ = ৫ X ১৭ X ৮৩
৮৮৫৫ = ৫ X ৭ X ১১ X ২৩
১২৭১৯ = ৭ X ২৩ X ৭৯
১৮০৯৫ = ৫ X ৭ X ১১ X ৪৭
২০৯৯৯ = ১১ X ২৩ X ৮৩
২২৮৪৭ = ১১ X ৩১ X ৬৭
২৯৩১৫ = ৫ X ১১ X ১৩ X ৪১
৩১৫৩৫ = ৫ X ৭ X ১৭ X ৫৩
৪৬০৭৯ = ১১ X ৫৯ X ৭১
৫১৩৫৯ = ৭ X ১১ X ২৩ X ২৯
৭৬৭৫১ = ২৩ X ৪৭ X ৭১
৮০১৮৯ = ১৭ X ৫৩ X ৮৯
৮১৭১৯ = ১১ X ১৭ X ১৯ X ২৩
৮৮৫৫৯ = ১৯ X ৫৯ X ৭৯
১০৪৬৬৩ = ১৩ X ৮৩ X ৯৭

এখানে উল্লেখ্য, পাঁচ উত্পাদকবিশিষ্ট সবচেয়ে ছোট লুকাস-কারমাইকেল সংখ্যা হচ্ছে ৫৮৮৪৫৫৷ আর ৫৮৮৪৫৫ = ৫ X ৭ X ১৭ X ২৩ X ৪৩৷
.................................................................................।

প্লাস্টিক নাম্বার

প্লাস্টিক নাম্বারের আরেক নাম প্লাস্টিক৷ আসলে X৩ = X + ১ সমীকরণটি সমাধান করে আমরা X-এর যে মান পাই তা-ই হচ্ছে প্লাস্টিক নাম্বার৷ আমরা প্লাস্টিক নাম্বার যদি চ দিয়ে বুঝাই, তবে



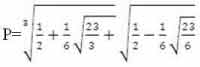
আর এই চ-এর মান যদি আমরা দশমিক ভগ্নাংশে প্রকাশ করি তাহলে-এর মোটামুটি মান হয় ১.৩২৪৭১৭৯৫ ৭২৪৪৭ ৪৬০২৫ ৯৬০৯০৮৮৫৪৷

কোনো কোনো সময় প্লাস্টিক নাম্বারকে সিলভার নাম্বার নামেও ডাকা হয়৷ তবে সিলভার নাম্বার নামটি সবচেয়ে বেশি ব্যবহার হয় সিলভাররেশিও বা সংখ্যাগে বুঝানোর জন্য৷ ১৯২৮ সালে Dom Hons Van Der Laan এ সংখ্যাটির নাম দেন প্লাস্টিক নাম্বার৷ প্রথমদিকে এর ওলন্দাজ নাম ছিল Plastische getal| গোল্ডেনরেশিও কিংবা সিলভার নাম্বার এই দুটি নাম থেকে আলাদাভাগে এর নাম প্লাস্টিক নাম্বার দেয়া হয়নি এ কারণে যে, এটি একটি বিশেষ পদার্থকে বুঝাবে, বরং প্লাস্টিক শব্দটির বিশেষণিক অর্থের দিকটা মাথায় রেখেই এ নাম দেয়া৷ এর প্লাস্টিক শরে বিশেষণিক অর্থ হচ্ছে ত্রিমাত্রিক আকার৷ মনে রাখতে হবে শুধু X৩ = X + ১ সমীকরণের সমাধানই প্লাস্টিক নাম্বার নয়৷ নিচে দেয়া সমীকরণসমূহের সমাধানও প্লাস্টিক নাম্বার৷

X৫ = X৪ + ১
X৫ = X২ + X +১
X৬ = X২ + ২X + ১
X৬ = X৪ + X + ১
X৭ = ২X৬ - ১
X৭ = ২X৪ + ১
X৮ = X৪ + X৩ + X২ + X + ১
X৯ = X৬ + X৪ +X২ + X +১
X১২ = X১০ - X৪ - ১
X১৪ = ৪X৯ + ১
..................................................................................।

বলুন তো কার ছবি : ২৬



ছবির এই মহিলা গণিতবিদের জন্ম ও বেড়ে ওঠা তাইওয়ানের কাউচিউংয়ে৷ জন্ম ১৯৪৯ সালের ৯ অক্টোবরে৷ এখনো বেঁচে আছেন৷ বাবা একজন প্রকৌশলী, ১৯৭৪ সালে গণিতে পিএইচডি করেন পেনসিলভানিয়া বিশ্ববিদ্যালয় থেকে৷ তার থিসিসের বিষয় : রামসে নাম্বারস ইন মাল্টি-কালারস৷ থিসিস সম্পাদন কনে হার্ভার্ট উইলফ-এর অধীনে৷ ২০ বছর কাজ করেন বেললেবস এবং বেলারে-এ কম্বিটেরিজ বিষয়ের ওপর৷ ১৯৯৫-এ ফিরে যান পেনসিলভানিয়া বিশ্ববিদ্যালয়ে গণিতের অধ্যাপক হিসেবে৷ এরপর ১৯৯৮ সালে সানদিয়াগোর ইউনিভার্সিটি অব ক্যালিফোর্নিয়ায়৷ তিনি গণিতের ওপর ২০০-র মতো গবেষণা প্রবন্ধ লিখেছেন৷ গ্রাফ থিওরির ওপর লিখেছেন দুটি বই৷ তার গবেষণার ক্ষেত্র স্পেক্ট্রাল গ্রাফ থিওরি, ডিসক্রিট জিওমেট্রি, এলগরিদম ও কমিউনিকেশন নেটওয়ার্ক৷ ১৯৯০ সালে পান আলেন্ডায়িফার পুরস্কার, আমেরিকার ম্যাথামেথিক্যাল অ্যাসোসিয়েশন তাকে এ পুরস্কার দেয় গণিতের ওপর তার একটি চমত্কার লেখার জন্য৷ আরো দুজরে সাথে মিলে তিনি এ লেখা লিখেন৷ বলুন তো কে এই।
.................................................................................।

গত সংখ্যার ছবি : ২৪-এর উত্তর

গত সংখ্যার ছবিটি ছিল গণিতবিদ বেন ডেসকার্টস-এর৷ সঠিক উত্তরদাতার নাম মুশফিকুর রহমান, নিউ রোজডেল ইংলিশ স্কুল, প্রযত্নে- মজিবুর রহমান, রোড-৬, বাড়ি-১৪, সোনাডাঙ্গা আ/এ, খুলনা৷

আপনার ঠিকানায় এ সংখ্যা থেকে শুরু করে আগামী ৬ মাস বিনামূল্যে কমপিউটার জগৎ পৌঁছে যাবে।