২-এর বর্গমূল ও ‘সোনালি আয়তক্ষেত্র’ (গত সংখ্যার পর)

কী করে গ্রিকরা ২ সংখ্যাটিকে তাদের ভাবনায় প্রথম স্থানে নিয়ে আসেন? বাস্তব জগতে এই ২-এর কী কোনো অস্তিত্ব রয়েছে? হ্যাঁ, রয়েছে। একটা মেঝের কথা ভাবুন, যার ওপর বসানো আছে টাইল। আর এই টাইলগুলো অর্ধ-বর্গ বা হাফ-স্কয়ার। আমরা যদি মনোযোগ দিয়ে তা দেখি, তবে দেখবো মধ্যখানে একটি সমকোণী ত্রিভুজ, আর এর প্রতিটি বাহুতে রয়েছে এক-একটি বর্গ।



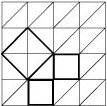
গ্রিকরা জানতেন পিথাগোরাসের উপপাদ্য-‘সমকোণী ত্রিভুজের অতিভুজ বর্গ এর অন্য দুই বাহুর বর্গের সমষ্টির সমান’। এরা জানতে পেরেছিল ৩, ৪ ও ৫ একক দৈর্ঘ্যবিশিষ্ট বাহুর একটি ত্রিভুজ সব সময় সমকোণী ত্রিভুজ হয়। কারণ, ৩২+৪২ = ৫২। একইভাবে এরা জানতো ৫, ১২ ও ১৩ একক দৈর্ঘ্যবিশিষ্ট বাহুর ত্রিভুজটিও একটি সমকোণী ত্রিভুজ। কারণ ৫২+১২২ = ১৩২। কিন্তু গ্রিকরা দেখলেন উল্লিখিত অর্ধ-বর্গ অর্থাৎ সমকোণী ত্রিভুজ আকারের টাইলের বাহুগুলোর দৈর্ঘ্য যথাক্রমে ১, ১ ও ২। কারণ ১২+১২ = (২)২। এটি অবশ্যই সত্য, কারণ পিথাগোরাসের উপপাদ্য সত্য। সে অনুযায়ী এখানে টাইলটি অর্ধ-বর্গ হওয়ায় এই অর্ধ-বর্গ তথা ত্রিভুজটি একটি সমকোণী ত্রিভুজ। আর সে কারণেই এ ত্রিভুজের দীর্ঘতম বাহু তথা অতিভুজটির বর্গ অপর দুই বাহুর বর্গের সমষ্টির সমান হবে। ১২+১২ হবে (২)২-এর মানের সমান। বলা সেজন্য ২ সংখ্যাটির একটি নাম দেয়া হয়েছে পিথাগোরাস ধ্রুবক বা কনস্ট্যান্ট। আসলে ২ হচ্ছে একটি সমদ্বিবাহু সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য, যে ত্রিভুজটির সমান বাহু দুটির দৈর্ঘ্য একক দৈর্ঘ্যবিশিষ্ট। যাই হোক, গ্রিকরা আরো লক্ষ করলেন, অর্ধ-বর্গ বা সমকোণী ত্রিভুজাকার প্রতিটি টাইলের অতিভুজ বাহুটির দিকের বর্গটিতে রয়েছে পুরো ৪টি টাইল, আর অন্য দুটি বাহুর দিকের প্রতিটি বর্গে রয়েছে ২টি করে টাইল। অতএব দেখা গেলো, একটি সমকোণী ত্রিভুজের দুই বাহুর দৈর্ঘ্য প্রতিটি ১ একক করে হলে এর অতিভুজটির দৈর্ঘ্য হতে হবে ২। কারণ, ১২+১২= (২)২। এই ফ্লোর টাইলগুলো বাস্তব জগতেরই অংশ। অতএব গ্রিকরা বললেন ২ একটি বাস্তব সংখ্যা বা রিয়েল নাম্বার। কিন্তু এটি মূলদ সংখ্যা নয়। এটি একটি অমূলদ সংখ্যা।

একটা প্রশ্ন হচ্ছে ২-এর মান কত? কাছাকাছি মান ধরলে ভগ্নাংশ আকারে ২-এর মান ৯৯/৭০। মনে রাখতে হবে, এই মান ২-এর একদম সঠিক বা যথার্থ কোনো মান নয়। যদি একদম সঠিক মান তাই হতো, তবে তো আমরা ২-কে মূলদ সংখ্যাই বলতে পারতাম। কারণ, কোনো সংখ্যাতে দুই পূর্ণ সংখ্যার অনুপাত তথা ভগ্নাংশ আকারে যথার্থভাবে প্রকাশ করতে পারলে তা মূলদ সংখ্যা বা র্যাখশনাল নাম্বার হয়ে যায়।

যাই হোক, আমরা ২-এর মান আসন্ন ৬৫ দশমিক স্থান পর্যন্ত যদি বের করি তবে ২ = ১.৪১৪২১ ৩৫৬২৩ ৭৩০৯৫ ০৪৮৮০ ১৬৮৮৭ ২৪২০৯ ৬৯৮০৭ ৮৫৬৯৬ ৭১৮৭৫ ৩৭৬৯৪ ৮০৭৩১ ৭৬৬৭৯ ৭৩৭৯৯ (৬৫ দশমিক স্থান পর্যন্ত)। ২-এর সঠিক মান বের করতে গিয়ে এ ধরনের আসন্ন মান নিয়ে আমরা কি সন্তুষ্ট থাকতে পারি? আমরা সাধারণত দুই দশমিক স্থান পর্যন্ত আসন্ন মান ধরে থাকি। সে অনুযায়ী ২-এর মান কমের পক্ষের হবে ১.৪১ এবং বেশির পক্ষে ১.৪২। যদি ২ = ১.৪১ হয় তবে (২)২ = (১.৪১)২, অথবা ২ = ১.৯৮৮১, বা ২-এর চেয়ে সামান্য কম।

আবার ২ = ১.৪২ হলে, (২)২ = (১.৪২)২, অথবা ২ = ২.০১৬৪, যা ২-এর সামান্য বেশি।

অতএব ২ একটি মূলদ সংখ্যা নয়, তেমনি ৫ কি ৩ সংখ্যা দুটিও মূলদ নয়। তবে ৪ অবশ্যই মূলদ সংখ্যা। ২, ৩,৫ ইত্যাদি অমূলদ সংখ্যা হলেও এদের বাস্তব ব্যবহার রয়েছে অনেক, যেমন tan 45 = 1/2, sin60 = 3/2, গোল্ডেন অনুপাত = (১+৫)/২।

এর বাইরেও ২-এর অনেক বাস্তব ব্যবহার রয়েছে। ব্রিটেন ও ইউরোপের দেশগুলোতে এবং আমাদের এ দেশের নানা সাইজ বা আকারের কাগজের নাম হিসেবে আমরা এ-জিরো, এ-ওয়ান, এ-টু, এ-থ্রি, এ-ফোর ইত্যাদি নাম ব্যবহার করি। আমরা কমপিউটারে এ-ফোর সাইজের কাগজ ও ফাইল অহরহ ব্যবহার করছি। এ-জিরো কাগজের আকার হচ্ছে ১ বর্গমিটার। এখন এ-জিরো কাগজটি অর্ধভাঁজ করলে আমরা এ-ওয়ান আকারের কাগজটি পাবো। আর এ-ওয়ান কাগজকে অর্ধভাঁজ করলে পাবো এ-টু আকারের কাগজ। এভাবে সামনে চলতে থাকবে। মজার ব্যাপার হলো, এখানে সব আকারের কাগজের শেপ বা ধরনটা হবে একই ধরনের। এসব প্রতিটি আকারের কাগজে দৈর্ঘ্য ও প্রস্থের অনুপাত হবে ২ : ১। কোনো আয়তক্ষেত্রের বাহু যদি এ ধরনের অনুপাতে হয় তখন এই আয়তক্ষেত্রকে বলা হয় golden rectangle। বাংলায় আমরা এর নাম দিতে পারি ‘সোনালি আয়তক্ষেত্র’। তাহলে দেখা গেলো ২ সংখ্যাটি জাদুকরিভাবে উপস্থিত রয়েছে আমাদের পরিচিত কাগজের আকারেও। হয়তো আগামী দিনে সঠিক গণিতবিদদের গবেষণা থেকে ২ সংখ্যাটির নানা রহস্য ও সুন্দর দিক আমরা জানবো। গণিতপ্রেমী মানুষই শুধু সম্ভব করে তুলবেন সে বিষয়টিকে। সে আশা আমরা করতেই পারি। তবে শেষ করার আগে ২ সম্পর্কে আরেকটি তথ্য জানিয়ে দিই- ব্যাবিলনীয়রা ২-এর একটা আকর্ষণীয় মান প্রকাশ করতে পেরেছিলেন, তা হলো :

২৪ ৫১ ১০
২ = ১ + + + = ১.৪১৪২১২৯৬২৯৬২৯৬...
৬০ ৬০২ ৬০৩